Excluded Volume and ExpaNSION fACTOR of Polymers

It is well known that the size of a polymer depends on the type and temperature of the liquid in which it is placed. In a good solvent, a polymer coil will expand (swell) due to the affinity with the solvent molecules, whereas in a poor solvent the polymer coil will shrink, i.e., it will avoid mixing with solvent molecules. 

To calculate the degree of swellling of a polymer coil in a solvent, we assume that the polymer segments and the solvent molecules are randomly distributed in the coil volume R³, and that the heat of mixing is proportional to the volume fraction of polymer segments in R³. Let us also assume that the polymer is in a state where its end-to-end distance R is close to its most probable value, lN^α, where l is the (average) length of a repeat unit and N is the number of repeat units in the polymer chain. These are crude assumption; nevertheless, the formulas that can be derived from it, describe, at least semi-qualitatively, the correct behavior of polymer chains immersed in solvent.

For this case, the probability W(R) of a chain having size R is proportional to the product of the following three factors:

W(R) ∝ P(R) · Q(R) · S(R)

or

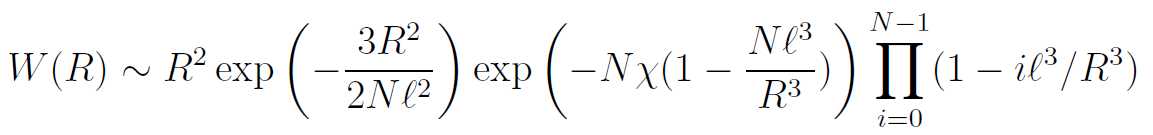
The first factor, P(R), is the probability distribution of the end-to-end distance of an ideal chain, the second factor, Q(R), describes the solvent-polymer interaction (Boltzman factor) and the third, S(R), is the probability that the configurations described by the first factor are also allowable under excluded volume conditions (excluded volume correction).

To estimate the average or statistical size of a polymer chain we have to calculate the value R that makes W a maximum. If the volume fraction of polymer segments in the sphere of radius R is small, then the approximation 1 - x ≈ e^-x is valid and we obtain

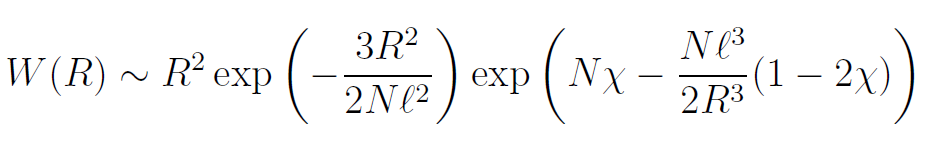
The maximum of W can be found by differentiating the logarithm of the equation above. This gives

The first term describes the elastic deformation of the chain, and the second term describes the swelling of the coil due to excluded volume interaction and mixing with solvent molecules. The expression above can be rewritten in the form:¹

α⁵ - α³ ≈ 4/3 ·z

where α =R^1/2 /N^1/2l is the swelling coefficient, z = (1 - 2χ)N^1/2 = v N^1/2l^-3 is a numeric factor describing binary collisions of molecules, and  v = l³(1 - 2χ) is the so-called excluded volume parameter. The result is similar to that of Flory (1949) who found following expression:²

α⁵ - α³ ≈ 2.598 ·z

whereas the perturbation theory of Fixman (1955) yields:³

α²  ≈ 1 + 4/3 ·z - (16/3 - 28π/27) z² + ...

All three expression are in good agreement for very small expansions (small z values) but yield very different swelling coefficients (α) for larger z values (see Figure below).

 

 

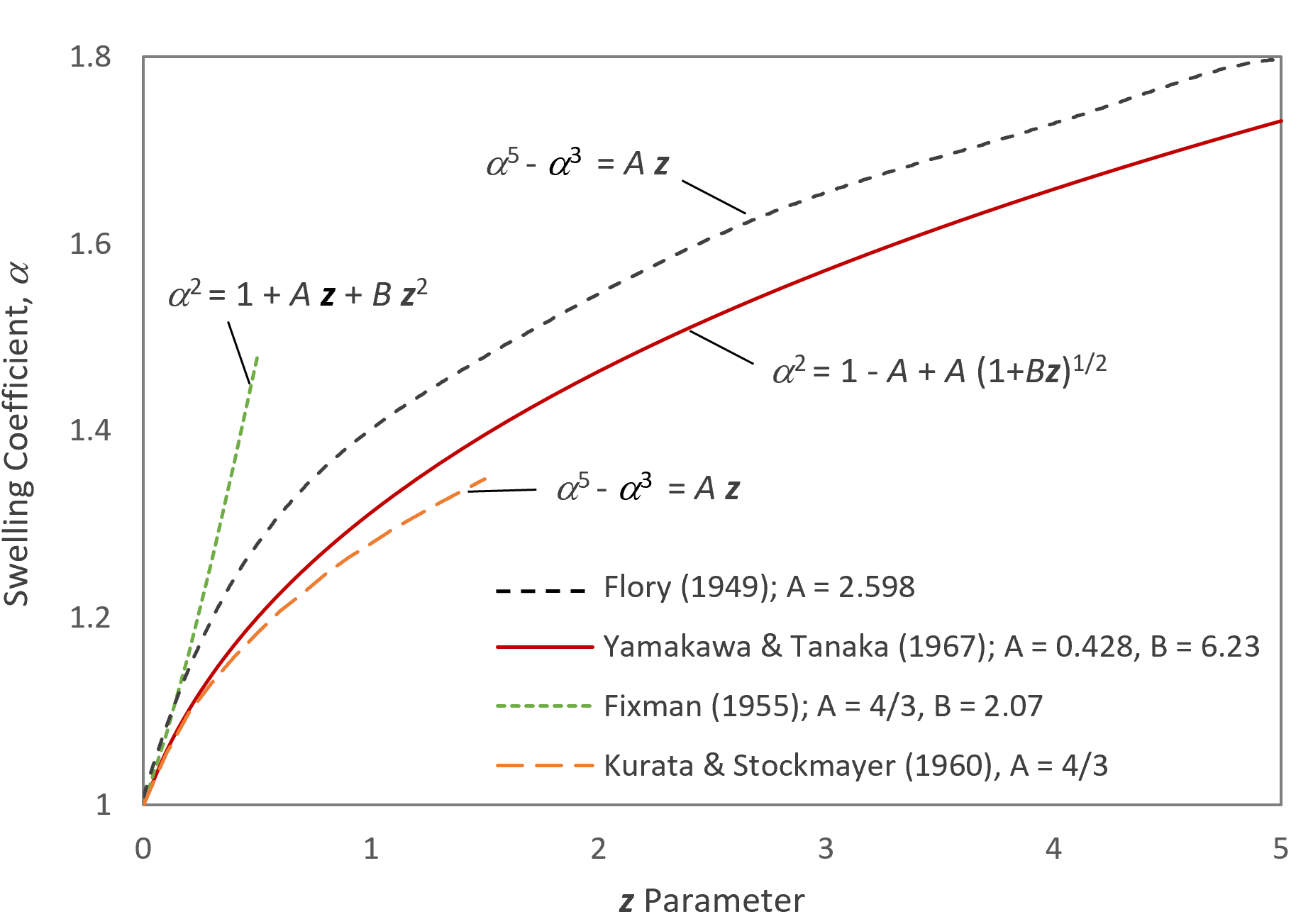
We believe one of the most accurate equations for the swelling coefficient can be derived from the Yamakawa-Tanaka theory^4,5: 

α²  ≈ 0.572 ·z - 0.428 (1 + 6.23 z)^1/2 + ...

For small z values, Kurata's and Stockmayer's solutions are in good agreement with the solution of Yamakawa and Tanaka whereas Flory's and Fixman's model predict much larger swelling coefficients (see Figure above).

 

Size of Polymer Coil

The size of a polymer coil can be estimated from the mean-field solution⁷

α⁵ - α³ ≈ (1 - 2χ) N^1/2

For example, in a good solvent, α > 1, χ is small or negative, indicating strong (polar) attractions between the polymer and solvent molecules. Under these conditions, a polymer coil will expand and dissolve in the solvent due to its affinity with the solvent molecules. For this case, the second term on the left-hand side (α³) can be neglected if N >> 1. It follows

R ∝ N^3/5 (1 - 2χ)^1/5 = N^3/5 v^1/5

The value of the exponent, ν = 3/5, is not the exact value but very close to it. Calculation based on renormalization group methods give a more accurate value of ν = 0.588.

In a poor solvent, χ is large and polymer-solvent contacts are unfavorable. Under these condtions a polymer will avoid to mix with solvent molecules and the coil will be more compact and at a certain point, it will be immiscible with the solvent, i.e. the coil will collapse (globule state). Thus, α << 1 and α³ ≈ 4/3 ·z. In this case we find

R ∝ N^1/3 (-v)^-1/3

 

Theta-Temperature And Coil-Globule Transition

With increasing temperature, v will change sign from positive to negative. The temperarue where the excluded volume parameter v equals zero is called the θ temperature. At this temperature, the repulsive excluded-volume forces balance the attractive forces between the segments and the polymer coil behaves like an ideal polymer or a Gaussian chain with unperturbed dimensions, which are the same as those of a polymer in its melt state:

α_θ = R^1/2 / N^1/2l  =  1

Below the θ temperature, the size of the polymer is much smaller than an ideal chain and at a certain point, the polymer coil will collapse, i..e expel all solvent molecules. This change is called coil-globule transition.

In terms of the phase equilibrium of a poor-solvent-polymer mixture, the θ-temperature is equal to the critical miscibility temperature in the limit of infinite molecular weight.

At the θ-temperature, the intrinsic viscosity η is proportional to the unperturbed dimension or mean square end-to-end distance.

References & Notes

1. M. Kurata, W. H. Stockmayer, A. Roig, J. Chem. Phys. 33, 151 (1960)

2. P. J. Flory, J. Chem. Phys. 17, 303 (1949) and P.J. Flory, T.G. Fox, J. Am. Chem. Soc., 73, 1904 (1951)

3. M. Fixman, J. Chem. Phys. 23, 1656 (1955); 36, 3123 (1962)

4. H. Yamakawa, G. Tanaka, J. Chem. Phys. 47, 3991 (1967)

5. Hiromi Yamakawa, Modern Theory of Polymer Solutions, Harper & Row, London 1971

6. A good overview of the older models is given in Yamakawa's famous book "Modern Theory of Polymer Solutions".⁵ So far, there is no exact treatment of self-avoidance for long chain molecules.

7. The mean field theory (also known as self-consistent field theory) describes the behavior of complex systems by replacing it with a simpler one. The effects caused by the interactions of a large number of small individual components is approximated by a single averaged effect, which reduces a many-body problem to a simple one-body problem.